Интернет магазин китайских планшетных компьютеров |
|||||||||||
Компьютеры - Троичные функции - Троичные логические функции23 января 2011Оглавление: 1. Троичные функции 2. Троичные логические функции 3. Бинарные троичные логические функции 4. Тринарные троичные логические функции 5. N-арные троичные логические функции Нульарные троичные логические функцииНульарные троичные логические операции с унарным выходомВсего существуют
В троичной симметричной системе счисления:
Унарные троичные логические функцииУнарные троичные логические функцииВсего существует Так как возможны более сложные функции дающие при подаче на вход одного трита тот же результат, что и простейшие унарные троичные функции, то число более сложных троичных функций с нижеприведёнными результатами от одного трита теоретически бесконечно.
Любую унарную троичную функцию можно выразить используя две другие унарные базисные троичные функции, одна из которых — любой из двух циклических сдвигов, а другая — любой из трёх обменов. Эти пары функций образуют множество из шести унарных троичных базисов. Любой из трёх обменов производит переход от одного из двух вращений к противоположному вращению. Любой из двух сдвигов обеспечивает вращение в одном из двух направлений на 1/3 оборота, на 2/3 оборота и на 3/3 оборота.
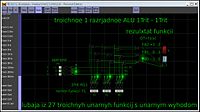
Снимок модели троичного унарного с унарным выходом АЛУ в трёхбитной одноединичной системе троичных логических элементов в логическом симуляторе Atanua
Все 27 унарных троичных операций выполняются троичным унарным с унарным выходом АЛУ в трёхбитной одноединичной системе троичных логических элементов, снимок модели которого в логическом симуляторе Atanua приведён на рисунке справа, и записываются в троичный триггер с соответствующей логикой управления. ОбозначенияДля обозначения унарных троичных функций достаточно любых трёх троичных знаков, 4/3 девятеричного знака или одного двадцатисемеричного знака, следовательно, так как возможно бесконечное количество таких знаков, возможно бесконечное множество обозначений унарных троичных функций. Из этого множества обозначений числовые обозначения по результатам действия функций являются естественными обозначениями. Цифровые обозначения могут быть постфиксными надстрочными, строчными и подстрочными и префиксными надстрочными, строчными и подстрочными, при этом для надстрочных и подстрочных обозначений нужно набирать пять знаков для открывающих и шесть знаков для закрывающих скобок, поэтому проще цифровые строчные обозначения с обычными скобками. Grabb использует для обозначения шесть знаков: ∪, ∩, ↘, ↗, A, A, из которых 5 труднонабираемы на клавиатуре. Шесть знаков могут выразить до 6²=36 функций, тем не менее Grabb использует для обозначения −7, −3, 3 и 7 функций четыре знака, что относительно избыточно. Mouftah использует для обозначения 16 знаков: ¬, ¬, ⌐, ⌐, ┘, ┘, └, └, ⊼, ⊽, 0, +,, A, A, из которых 11 труднонабираемы на клавиатуре. Два шестнадцатеричных знака могут выразить до 11²=256 функций, тем не менее для −6 и −2 функций Mouftah использует 11 знаков, что относительно избыточно. Yoeli обозначает положительные декодеры −1, 0 и +1 с двумя i тремя труднонабираемыми на клавиатуре надстрочными индексами, при этом не описываются положительные декодеры с двумя 0, нулевые декодеры с двумя 1 и с двумя −1, отрицательные декодеры с двумя 0 и с двумя 1. В симметричной троичной системе:
При замене знака i на знак 2 получается таблица унарных троичных функций в несимметричной троичной системе {2,0,1}. Троичная логическая тождественная функцияТроичный логический повторитель. Является простейшей линией задержки. ИнверсииИнверсии и неполные обменыВ троичной логике неполные обмены и инверсии совпадают. В четверичной логике два единичных дигональных обмена и два парных недиагональных обмена являются инверсиями, остальные неполные обмены инверсиями не являются. В пятеричной логике для инверсии необходимы два парных обмена в которых в сумме участвуют значения четырёх вершин. В шестеричной логике для инверсии необходимы два парных обмена или три парных обмена. В семеричной логике для инверсии необходимы три парных обмена в которых в сумме участвуют значения шести вершин. В N-ичной логике для инверсии в обмене участвуют значения N-1 вершины. В нечётных логиках по отношению к одной вершине возможна одна инверсия. В чётных логиках по отношению к одной вершине возможны две инверсии: диагональная и перпендикулярная. Инверсии в троичной логикеТроичные инвесии — унарные операции, меняющие местами два из трёх логических состояний. NOTL- = ROTB Традиционная инверсия, неполное отрицание, не влияющее на состояние «неизвестно», в троичной логике называют отрицанием Лукасевича и обозначают как ~Lx. Функция инверсии Лукасевича входит в логику Клини. В симметричной троичной системе счисления Фибоначчи такое отрицание просто изменяет «знак» троичного разряда, в несимметричной троичной системе счисления знак троичного разряда не изменяется. 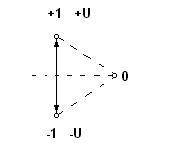 Граф переходов в операции отрицания Лукасевича — одно ребро треугольника с двухсторонними переходами от 1 к −1 и обратно. Операция линейная, одномерная, из линии в плоскость не выходит. Кроме традиционной инверсии Лукасевича, выделяют ещё две операции инверсий, которые обозначают как NOT и NOT. Первая сохраняет неизменным состояние −1, а вторая сохраняет +1, при этом операции по-разному действуют на состояние 0:
в несимметричной троичной системе счисления с соответствием {-1,0,+1} — {2,0,1}:
так как возможны шесть соответствий троичной симметричной системы счисления и троичной несимметричной системы счисления:
то в несимметричной троичной системе счисления с другими соответствиями троичной симметричной системе счисления таблицы функций NOTL0, NOTL- и NOTL+ будут другими;
Граф операции NOT — одно ребро треугольника с двухсторонними переходами от 0 к 1 и обратно. Циклические сдвигиСдвиги и инверсииВ двоичной логике сдвиги и инверсии совпадают и выражаются одной операцией сдвига на 180° или инверсии — NOT. В троичной и более значных логиках сдвиги и инверсии являются разными функциями. Сдвиги не меняют направления вращения. Операцию сдвига выполняют регистры сдвига. Инверсии меняют направление возрастания значений при правом обходе вершин графа. Операцию инверсии выполняют только триггеры. В многозначных логикахВ троичной логике существует закон тройного сдвига: SHIFT1F)) = X, В четверичной логике существует закон четверного сдвига: SHIFT1F))) = X, В пятеричной логике существует закон пятерного сдвига: SHIFT1F)))) = X, … В N-ичной логике существует закон N-ного сдвига: N сдвигов вперёд равносильны повторению, В-ичной логике существует закон-ного сдвига: сдвигов вперёд равносильны повторению, … Обобщение: В объёмных логиках место окружности занимают многомерные сферы. Сдвиги в троичной логикеЛогические циклические сдвиги вперёд и назад. Если рассмотреть многовершинные графы, то в них возможны циклические сдвиги на 1 вперёд и назад и инверсии. Сдвиги не являются инверсиями и отличаются от функции инверсии и NOT). Они более просты, ближе к логике работы троичного триггера и более полно описывают возможные переходы в троичном триггере. В проекте Стива Грабба эти функции называются вращение вверх и вращение вниз.
или в троичной симметричной системе {-1,0,+1}:
Графы операций логических циклических сдвигов вперёд и назад — треугольники с односторонними переходами вправо или влево. Для обеих функций справедливы уравнения: Справедливы также следующие уравнения: Сдвиг на 2 равен двум сдвигам на 1: Только в троичной логике сдвиг в одну сторону на 2 равен сдвигу на 1 в другую сторону: Унарные троичные логические функции с бинарным результатомВсего существует К этим функциям относятся демультиплексоры и дешифраторы с бинарным выходом. Унарные троичные логические функции с тринарным результатомВсего существует К этим функциям относятся демультиплексоры и дешифраторы с тринарным результатом. Троичный дешифратор «1 трит в 3 строки»Можно рассматривать как объединение трёх унарных троичных функций с унарными результатами из таблицы 1.
Унарные троичные логические функции с m-арными выходамиВсего существует К этим функциям относятся демультиплексоры и дешифраторы с m-арным результатом. Просмотров: 9538
|
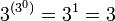 простейшие нульарные троичные функции.
простейшие нульарные троичные функции.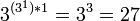 простейших унарных троичных функций.
простейших унарных троичных функций.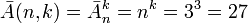
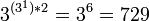 простейших унарных троичных функций с бинарным выходом.
простейших унарных троичных функций с бинарным выходом.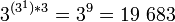 простейших унарных троичных функций с тринарным выходом.
простейших унарных троичных функций с тринарным выходом.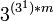 простейших унарных троичных функций с m-арным выходом, то есть бесконечное число.
простейших унарных троичных функций с m-арным выходом, то есть бесконечное число.